There Are Four Seasons

This post is a response to Nate Soares  claiming that there are only two seasons. It feels strange to produce a counter to something this low on the controversy-scale. I mean, the weather (and by extension the changing seasons) is the poster child of innocuous conversation topics nobody gets riled up about. But the reasoning touched on a philosophical topic that’s sort of an obsession of mine  and the interesting argument stayed with me.

I came up with what I think is an elegant model of why Soares is totally wrong (I’m really trying to up the controvery here) and now I can’t help myself.

His point is that we’re making a mistake when we say that there are four seasons, since spring and autumn shouldn’t count. Why? Because dividing the yearly cycle of the sun in the sky into four parts doesn’t carve reality at its joints; it doesn’t have four natural parts that correspond to our idea of the seasons. He shows this graph

and asks if there really are four parts here. The answer is no, there seems to be only two main parts, two seasons – summer and winter, majority bright and majority dark. What if you try to divide it into four parts? Which division neatly carves the cycle?

Soares suggests this:

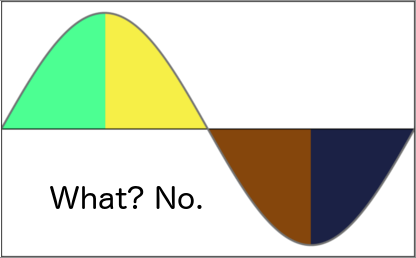
Which does seem like the only way to do that makes sense. But then we should consider “summer” to start in midsummer and be characterized by shortening days, and we should consider midwinter the start of winter, winter being thought of as “the season when things get brighter”, which Soares thinks is silly and strange.

I’m not sure if he means that people do think of the seasons as corresponding to these periods, or just that we should if we want to divide the cycle in natural parts (there might be cultural differences here). In any case, I agree that this division is, to use a technical term, stupid.

Winter is clearly centered on the trough of the cycle and summer on the peak, leaving no way to carve out “spring” and “autumn” as additional seasons in a way that aren’t shamefully un-elegant.

Or does it?

We put things into different categories when they have different salient properties. So if we have four seasons there should be four defining characteristics. Soares claims there are only two: more dark than bright and more bright than dark, with the border at the parity line. But things are not so much defined by their borders as by their centers.

The centers of  summer and winter are the extreme values of the cycle, maximum and minimum. Being maximally or minimally something are conspicuous properties. Being close to the midpoint is not—that’s the opposite of a conspicuous property. The ratio between darkness and light is much less noticeable when it is not extreme; you barely notice when it passes through exact parity.

What is extreme about those parts of the cycle is the rate of change, not the value. The yearly cycle, as drawn here, is a sine curve. Its rate of change over time is given by its derivative, which is a cosine curve.

Here is the “seasonal sine curve” with its derivative the cosine curve (red) superimposed:

Since we featherless bipeds care about the darkness and the light and it’s rate of change, both the light-darkness curve and its derivative should be used in segmenting the cycle. It’s not cheating. I’m not adding anything new; the derivative is a property of the curve itself.

Now, we’re interested in extreme values, which correspond to striking properties. Right now we care less about whether those extreme values are maxima or minima. If we transform the curves to show just their magnitudes, irrespective of direction, we get this:

What do we find? Look! Four humps. Well, three and two halves, but you get the point. Here are our seasons:

Winter turns into spring when the “it’s getting lighter” property gets more noticeable than the “it’s dark” property, and spring turns into summer when the “it’s bright” aspect overtakes the “it’s getting brighter” aspect.

Did you enjoy this article? Consider supporting Everything Studies on Patreon.